Introduction

Scientific and technical communities trend toward obtaining novel macro-structural material responses via micro-structural design. Achieving these new material properties is expected to highly impact the design of new devices in many fields of science and technology. Just to mention a few applications, the use of architectured materials results in:

1. Negative or null thermal expansion coefficients
2. Negative index of optical refraction (see Fig. 1)
3. Materials with negative Poisson’s ratio (NPR), also known as “auxetics”

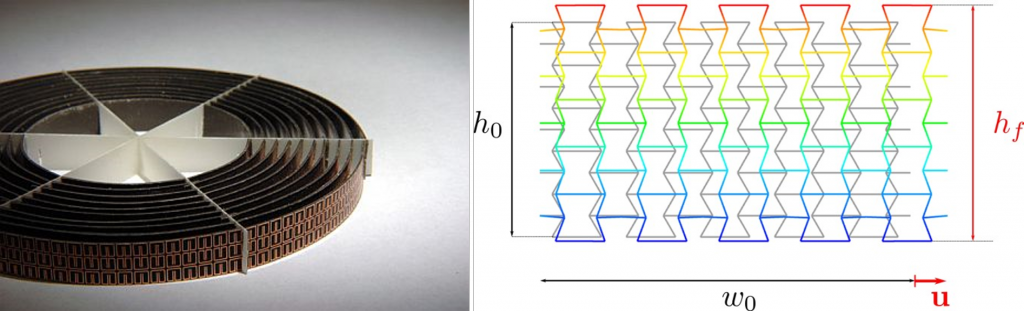
Fig. 1: (left) this periodic structure is practically invisible, if we could see the world in microwaves (wavelength: 3.5 cm), source: [1];
(right) auxetic material stretches in the vertical direction, perpendicular to the applied extension (horizontal).

Developing an architectured material with tailored properties implies an inverse problem: identifying the design parameters of a unit-cell, such that the desired properties at the bulk material are obtained when the cell is tessellated in space.

The main difficulty of handling a parametric description of the micro-structure and to determine its influence in the emerging properties of the bulk is the multidimensional character of the problem. The computational complexity increases exponentially with the number of parameters and hence the burden of the inverse problem.

Goal

One possible solution to affordably deal with the so-called curse of dimensionality is using Reduced Order Models (ROM). Here, we focus on the Proper Generalized Decomposition (PGD). This technique is especially well suited to simulate the behavior of the parametric structure (with parameters describing both geometrical and material properties of the cell) because it provides an explicit parametric solution (known as computational vademecum).

In the PGD philosophy, the computational vademecum is obtained once, often using High Performance Computing. Then, to solve the inverse problem, the parametric design space is browsed as a post-process, in a real-time phase providing very fast responses.

Results

An interesting application of these ideas is producing lattice materials that exhibit auxetic behavior using additive manufacturing (3D printing). The seed cell in this case is a parameterized structure as shown in Fig. 2, which describes its topology by means of four parameters (“b”, “a”, “α” and “t”). A periodic structure could be obtained by repeating the cell in the vertical and horizontal directions, and a tubular stent-like structure by wrapping it in a cylindrical shape (see Fig. 3).

Fig. 2: (left) parameterized unit-cell; (middle) periodic structure (rectangular array of cells); (right) stent-like cylindrical wrapping.

Fig. 3: auxetic tubular structures CAD & 3D printing.

Different numerical models have successfully predicted the material response of the bulk in this context [2]. However, the computational burden is still a bottleneck when the number of parameters is moderately large. Therefore, our PGD model efficiently deal with the parametric lattice structural problem (see Fig. 4). The explicit parametric solutions (computational vademecum) is to be exploited to derive the macro-scale properties of the resulting architectured material and hence to improve time performance in the inverse problem under consideration (see Fig. 5).

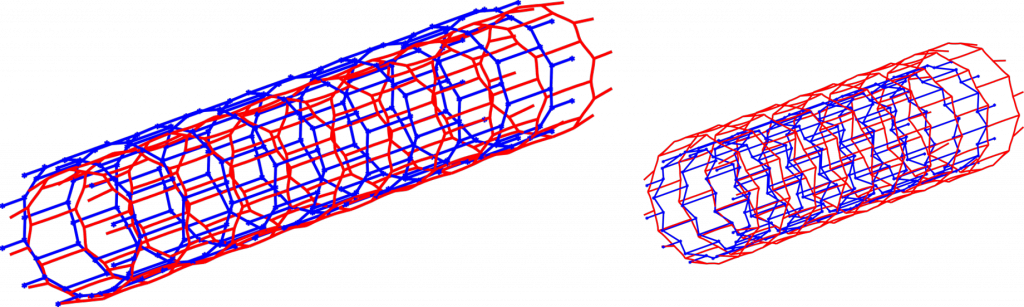
Fig. 4: axially loaded stent-like parametric structure solved by PGD. Computational vademecum provides real-time simulations for different combinations of the parameters.

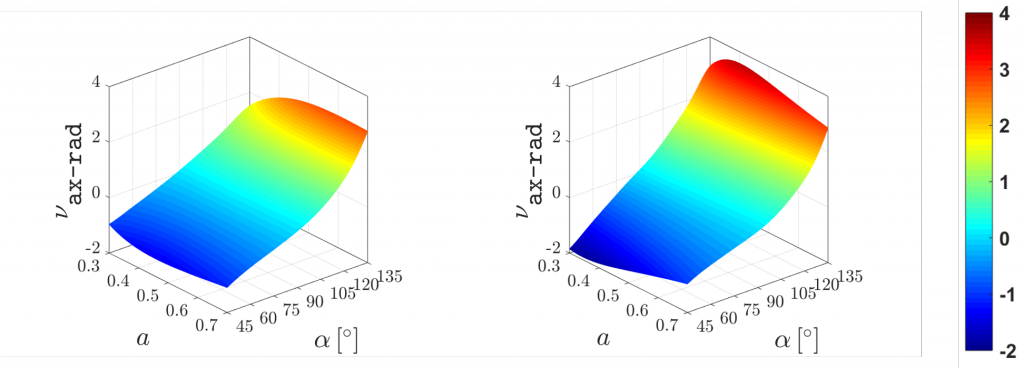
Fig. 5: PGD Poisson’s ratio “ν (axial-radial)” response against changes of parameters “a” and “α” (left and middle correspond to different combinations of parameters “b” and “t”).
Values in blue mean auxetic behavior: stent radius will increase for a given axial expansion, and the contrary happens for positive Poisson’s ratios.

Publications

Collaborations

Acknowledgements

References

[1] D. Schurig et al, Metamaterial electromagnetic cloak at microwave frequencies, Science, 314 (2006).

[2] J. Lee et al, A tubular biomaterial construct exhibiting a negative Poisson’s ratio. PLoS One, 11 (2016).